Projektowanie układów kombinacyjnych
Projekt, rysunki i kod strony: Michał Kubiś
| Wstęp | Przykład 1 - prostszy
| Przykład 2 - trudniejszy z dokładnym opisem| Minimalizacja funkcji przełączających | Realizacja układów kombinacyjnych z bramek
| Realizacja układów kombinacyjnych przy użyciu bloków funkcjonalnych
| Bibliografia
| (new) Ogródek - przykład 3
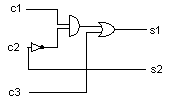
| WstępUkład kombinacyjny jest układem przełączającym (automatem cyfrowym) służącym do przetwarzania sygnałów dwuwartościowych. Sygnały wejściowe układu mogą pochodzić z czujników, wyłączników, przycisków itp. Sygnały wyjściowe mogą sterować np. lampkami sygnalizacyjnymi. Stan wyjść układu kombinacyjnego zależy tylko od aktualnego stanu wejść. Charakteryzuje się brakiem pamięci, która umożliwiłaby zapamiętywanie poprzednich stanów wejść.Zatem: wyjścia układu kombinacyjnego zależą (sa funkcją) tylko od wejść. 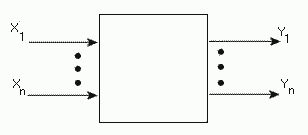 Układ przełączający można przedstawić w postaci bloku, mającego wejścia x1, x2, xn i wyjścia y1, y2, yn. Każde wejście może być w jednym z dwóch stanów 0 lub 1. Ciąg sygnałów wejściowych x1 ... xn określa stan wejść. Podobnie ciąg sygnałów wyjściowych y1 ... ymokreśla stan wyjść automatu. (x1, x2 ... xn)=X Przykład 1 - łatwiejszy - "na chłopski rozum"wymyślony przeze mnie, opisany przez uczniów VI L.O w Gdyni po korektach p. J.ŚmierzchalskiejUkład automatyki Tama na rzece posiada dwie śluzy s1 i s2 do regulacji poziomu wody jak pokazano na rysunku. W zależności od szybkości napływania wody do tamy, nadmiar wody jest spuszczany przez jedną ze śluz lub dwie śluzy jednocześnie. O aktualnym poziomie wody w tamie informują trzy czujniki (c1,c1,c3), które działają w momencie zalania ich przez wodę.
Czujniki zwracają wartość 1 gdy znajdują się pod poziomem wody (gdy są zatopione). 1. Zaprojektuj układ automatyki, który będzie sterował otwieraniem i zamykaniem śluz wg następujących zasad:
2. Sporządź zoptymalizowany układ oparty na bramkach NOT i do wyboru NAND lub NOR.
Rozwiązanie: 1. Tworzymy tabelę sterowania: (opisującą funkcje przełączające)
Stany niemożliwe takie jak 0 1 0; 0 0 1; 0 1 1; 1 0 1 są pomijane, czyli przyjmują stany dowolne.
2. Rysujemy tablicę minimalizacji (tablica Karnaugha): czyli:Dla śluzy pierwszej:
Jak wynika z tabeli funkcja zoptymalizowana ma postać: s1=c1 Tablica dla śluzy drugiej:
Tutaj minimalna postać funkcji: s2=c2.
Cały układ będzie więc miał postać:
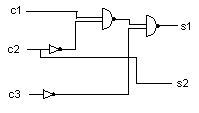
Po optymalizacji wszystkich bramek na NAND i NOT (z wykorzystaniem prawa deMorgana):
Przykład 2 - trudniejszy, ale z dokładnym opisem
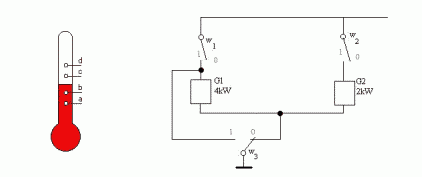
Przykładem automatu kombinacyjnego jest układ sterowania temperaturą. Pomiaru dokonujemy termometrem kontaktowym podający cztery sygnały: a, b, c, d, w 0 - jeśli temperatura jest niższa lub 1 - jeśli wyższa.
Ukaład posiada 2 grzejniki ( G1=4kW; G2=2kW ). Grzejnikami można sterować przy użyciu trzech wyłączników oznaczanych literą w (odpowiednio w1, w2 itd.). Zmienne wyjściowe w są funkcjami zmiennych wejściowych a, b, c, d. Funkcje te noszą nazwę funkcji przełączających, gdyż zarówno zmienne jak i funkcje mogą przyjmować tylko dwie wartości: 0 lub 1. Funkcje te nie są w pełni określone, gdyż nie wszystkie ciągi wartości zmiennych mogą się pojawiać na wejściu układu, lub też dla niektórych ciągów wartość zmiennych sygnału wyjściowego jest obojętna ( np.w3 dla abcd=1111). w2=F2(a,b,c,d) w3=F3(a,b,c,d) Ciąg wartości zmiennych będący ciągiem 0-1-wym może być traktowany jak liczba binarna; możemy też posługiwać się jej odpowiednikiem dziesiętnym (np. dla funkcji opisuj1cej w2). Dla określenia funkcji należy wypisać zbiór ciągów wartości zmiennych, dla których funkcja równa jest jedności oraz zbiór, w którym funkcja przyjmuje wartości 0. Ponadto dla funkcji nie w pełni określonych wypisujemy zbiór wartości zmiennych, dla których wartość funkcji jest nie określona. Postacią kanoniczną sumy nazywamy funkcję rozłożoną na sumę iloczynów, w których jako czynniki występują funkcje o liczbie argumentów o jeden mniejszej. Pełny iloczyn n zmiennych, jest to iloczyn zawierający wszystkie n zmiennych w postaci nie zanegowanej lub zanegowanej. Chcąc przedstawić funkcję przełączającą w kanonicznej postaci sumy, dla każdego ciągu ze zbioru F1 piszemy pełny iloczyn, w którym zerom ciągu odpowiadają zmienne zanegowane, a jedynkom - zmienne nie zanegowanej. Podobnie, chcąc przedstawić funkcję przełączającą w kanonicznej postaci iloczynu, dla każdego ciągu ze zbioru F0 piszemy pełną sumę, przy czym zerom ciągu odpowiadają zmienne nie zanegowane, a jedynkom - zanegowane. Możemy również dane wyrażenia poddać uproszczeniu stosując prawa algebry Bool'a - taką formę wyrażenia uproszczonego nazywamy wyrażeniem normalnym. Minimalizacja funkcji przełączających - cd. przykładu 2Tworzymy tablicę dla, przykładowo, przełącznika w2: 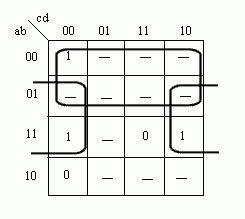 uzyskując funkcję w2= a negacja lub b i d negacja Poniżej pełny opis sposobu tworzenia i minimalizacji w takiej tablicy: Minimalizacja funkcji przełączającej polega na przedstawieniu jej w postaci normalnej, zawierającej możliwie najmniejszą liczbę zmiennych w celu ograniczenia ilości bramek niezbędnych do stworzenia danego układu. Początkową postacią funkcji jest albo tabelka wartości funkcji przedstawiona w postaci tzw.tablicy Karnaugha, albo zbiory F1, F0, FZ ( 1,0,Z - wykładniki ) ciągów wartości zmiennych, dla których funkcja przyjmuje wartość 1, 0 oraz nie określone. Minimalizację funkcji przełączających niewielkiej liczby zmiennych (do 5,6) najdogodniej jest przeprowadzić na tablicy Karnaugha. Tablica ta stanowi specyficzną odmianę tablicy wartości funkcji. Z boku tablicy wpisujemy wszystkie ciągi wartości dwu pierwszych zmiennych a, b - a u góry - wszystkie możliwe ciągi wartości pozostałych zmiennych c, d. Ciągi wartości zmiennych przedstawione są w takiej kolejności, że sąsiednie ciągi różnią się wartością tylko jednej zmiennej (ciągami sąsiednimi są również ciąg pierwszy i ostatni). W klatkach tablicy wpisujemy wartość funkcji przełączającej dla odpowiednich wartości argumentów. Jeżeli funkcja jest nie określona dla pewnych wartości zmiennych, to w tych miejscach tabelki stawiamy kreskę. Iloczyn czterech różnych zmiennych lub ich negacji (pełen iloczyn) przyjmuje wartości 1 dokładnie w jednym polu takiej tablicy. Iloczyn trzech zmiennych przyjmuje wartości 1 w dwóch polach, które albo sąsiadują ze sobą, albo leżą przy przeciwległych krańcach tablicy ( w obu przypadkach będziemy takie pola nazywać sąsiednimi). Wynika to z przyjętej kolejności ciągów wartości zmiennych a, b i c, d opisując tablicę. Iloczyn dwu zmiennych przyjmuje wartość 1 zawsze w czterech polach tablicy, zajmujących cały rząd pionowy lub poziomy albo tworząc kwadrat, leżący całkowicie wewnątrz siatki lub przechodzący przez jej klejone brzegi. Iloczynowi jednoczynnikowemu odpowiada osiem pól, leżących w dwu sąsiadujących ze sobą rzędach. 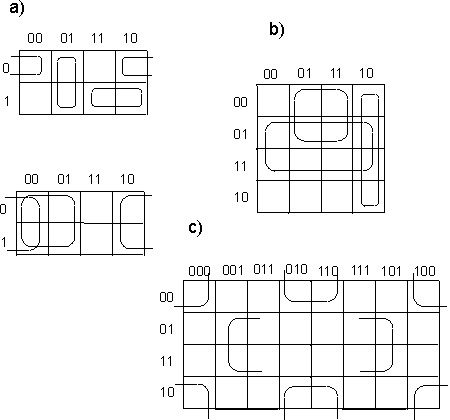 Przykłady tworzenia grup w tablicach KArnaugha zależności:
Realizacja układów kombinacyjnych z bramek - cd. przykładu 2W naszym przypadku uzyskujemy bezpośrednio z funkcji w2 (poz.1). Przerabiamy go bez zmiany wartości funkcji by uzyskać postać dogodną do wykorzystania prawa De'Morgana (poz.2) i wykorzystując je uzyskujemy postać oparta na bramkach NAND (poz.3) 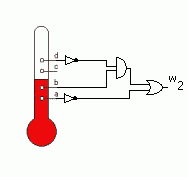 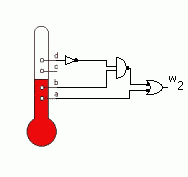 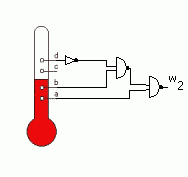
Poniżej opis zasad realizacji funkcji logicznych na bramkach:
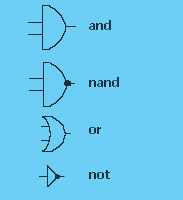
Element NOR realizuje funkcję negacji sumy oraz iloczynu negacji, a element NAND - funkcje negacji iloczynu oraz sumy negacji. Ponieważ element NAND realizuje zarówno negację iloczynu jak i sumę negacji zmiennych, i ma podwójne oznaczenie, wpisanie funkcji przełączającej realizowanej przez układ NAND jest bardzo proste. W układzie takim należy ponumerować kolejno warstwy (poziomy) elementów poczynając od wyjścia układu, po czym elementy NAND znajdujące się na poziomach nieparzystych należy narysować jako sumy negacji. Wówczas, pamiętając, że negacja na wyjściu elementu znosi się z negacją na dołączonym do niego wejściu, łatwo napisać funkcję realizowaną przez układ. 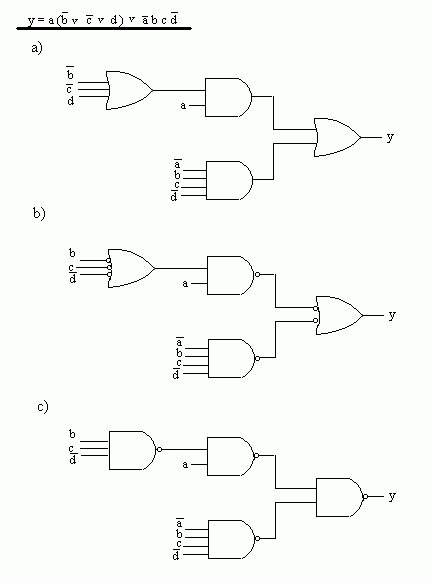 Przy syntezie układu złożonego z elementów NAND, realizującego daną funkcję przełączającą, należy narysować realizację danej funkcji na elementach sumy i iloczynu (rys. a), a następnie zastąpić iloczyny przez negacje iloczynów, a sumy przez sumy negacji , dodając jednocześnie negatory lub zanegowując zmienne wyjściowe, tak aby realizowana funkcja nie uległa zmianie (rys.b). Otrzymany układ jest złożony z elementów NAND. Niekiedy dla ujednolicenia schematu wszystkie elementy NAND rysujemy jako negacje iloczynu (rys. c). Realizacja układów kombinacyjnych przy użyciu bloków funkcjonalnychDowolny układ kombinacyjny może być zrealizowany przy użyciu pamięci stałej ROM, w której zapisane są tablice funkcji przełączających opisujących ten układ. Na wejścia adresowe pamięci podane są zmienne wejściowe, a wyjścia pamięci są wyjściami układu. Przy użyciu multipleksera z m-bitowym adresem można zrealizować dowolną funkcję przełączającą m zmiennych. Realizacja funkcji m zmiennych nie wymaga dodatkowych elementów. Używając tylko negatorów można zrealizować również dowolną funkcję m+1 zmiennych. Chcąc zrealizować wielowyjściowy układ kombinacyjny, opisany zespołem n funkcji przełączających tych samych zmiennych, trzeba użyć multipleksera komutującego słowa n-bitowe ( lub n multiplekserów 1-bitowych). Bibliografia
[1]W. Majewski: Układy logiczne. Warszawa WNT 1974. Przykład dodatkowy A - Ogódek
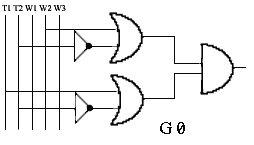
W pewnym ogródku botanicznym zainstalowano grzałkę, zraszacz, 2 czujniki
temperatury (T1,T2) oraz 3 czujniki wody (W1,W2,W3). Zależność
między czujnikami temperatury jest taka, że gdy T1 jest włączony -
jest zimno. Gdy oba są wyłączone - jest letnio. Gdy oba są włączone
jest ciepło, a wypadku, gdy T1 jest włączony, a T2 wyłączony - jest bardzo
ciepło.
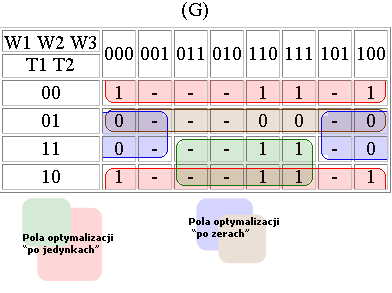
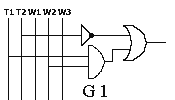
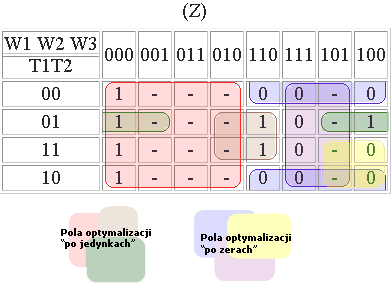
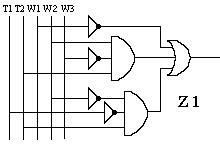
Optymalizacja zraszacza (Z):
|

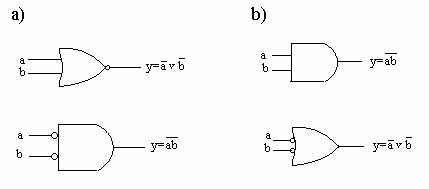 Układy kombinacyjne realizuje się za pomocą elementów logicznych - bramek, bloków funkcjonalnych (tj. multiplekser lub pamięć stała ). Podstawowymi elementami półprzewodnikowymi są w większości technik realizacyjnych elementy NOR lub NAND. Elementy NOR i NAND mają podwójne oznaczenia, gdyż zgodnie z prawem Morgana realizują funkcje zarówno sumy jak i iloczynu - to jest przyczyną ich uniwersalności.
Układy kombinacyjne realizuje się za pomocą elementów logicznych - bramek, bloków funkcjonalnych (tj. multiplekser lub pamięć stała ). Podstawowymi elementami półprzewodnikowymi są w większości technik realizacyjnych elementy NOR lub NAND. Elementy NOR i NAND mają podwójne oznaczenia, gdyż zgodnie z prawem Morgana realizują funkcje zarówno sumy jak i iloczynu - to jest przyczyną ich uniwersalności.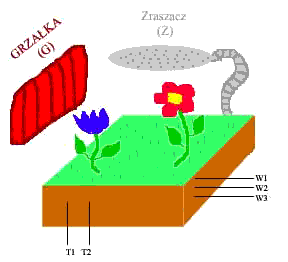
.gif)
.gif)